Search This Blog
Simplifying architecture to understand the art and science of designing beautiful structures. So, unleash your inner artist, create aesthetic designs and express your opinions in Facile Architecture. ;-)
Translate
Featured
- Get link
- X
- Other Apps
COMMON MATHEMATICAL EQUATIONS USED IN ARCHITECTURE
• FIBONACCI SERIES
Leonardo of Pisa (c. 1170 – c. 1250), also known as Fibonacci, was a medieval mathematician. As well as popularising the Arabic numeral system in Europe (at the time, Roman numerals were still used), he published a book called Liber Abaci , which contained the first mention of the mathematical sequence that bears his name. The Fibonacci sequence is one which starts with 0 and 1, and continues by adding the previous two numbers to get the next number in the sequence.
 |
| Fibonacci series Photo by: MicroOne |
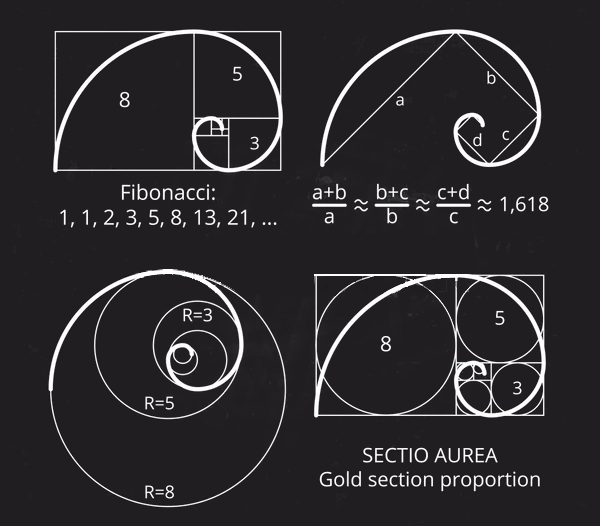
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones:
0,1,1, 2, 3, 5, 8,13, 21, 34, 55, 89
8 divided by 5 is 1.6
13 divided by 8 is 1.625
21 divided by 13 is 1.61538
34 divided by 21 is 1.61904
55 divided by 34 is 1.61764
• GOLDEN RATIO
 |
| Golden ratio Photo by: Rafael Javier |
Many artists, philosophers and architects over the centuries, from the ancient Greeks onwards, have believed that the proportions of the Golden Ratio are uniquely beautiful and pleasing to the eye. In other words, the rectangle above looks more beautiful than one where the longer side is twice the length of the shorter side, or so it is said.
 |
| The Parthenon, Athens Photo by: Adrian Balea |
Many of the artists and architects have even gone so far as to claim that these proportions were ordained by God; hence they are sometimes referred to as the Divine Ratio.
o In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0,
(a+b/a)=a/b=phiϕ
where the Greek letter phi ϕ represents the golden ratio.
o It is an irrational number with a value of:
(1+5^1/2)/2=1.618
o The golden ratio is also called the golden mean or golden section
Other buildings that exhibit these proportions include Paris’s Notre Dame Cathedral.
 |
| Notre Dame, Paris Photo by: Dyana Wing So |
This system of proportioning also seemingly appears in many works of art, especially from the Renaissance, when there was a resurgence of interest in art and science. For example, see Da Vinci’s Mona Lisa .
 |
| Mona Lisa Photo by: WikiImages |
There are many other examples of this proportioning in the Mona Lisa; her face, for example would fit neatly into a rectangle with sides based on the Golden Ratio. The series of rectangles that you can see superimposed on the Mona Lisa is linked to another aspect of the Golden Ratio, and points up its relationship with Fibonacci.
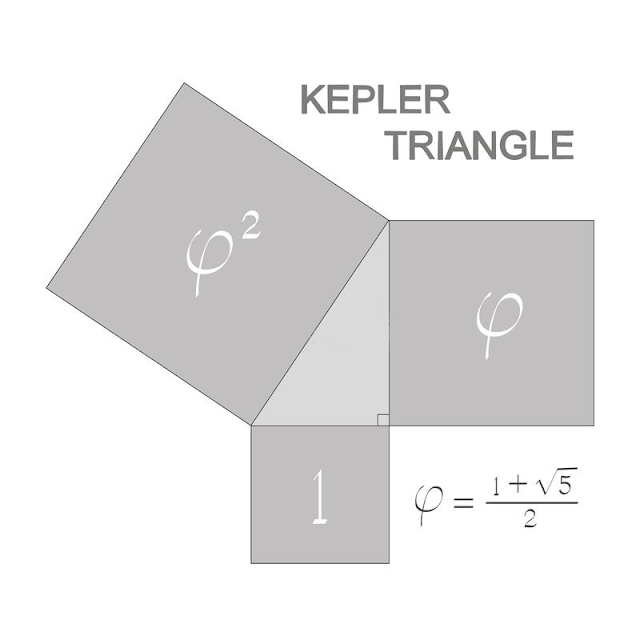
KEPLER TRIANGLE
o A Kepler triangle is a right triangle with edge lengths in geometric progression.
 |
| Kepler Triangle Photo by: Dreamsidhe |
o The ratio of the edges of a Kepler triangle is linked to the golden ratio and can be written
o 1 : 1.272 : 1.618.= 1: (ϕ^1/2): ϕ
o The squares of the edges of this triangle (see figure) are in geometric progression according to the golden ratio.
 |
| The Great Pyramid of Giza Photo by: Pete |
Base:hypotenuse (b:a) ratios for pyramids like the Pyramid of Khufu could be: 1:φ (Kepler triangle), 3:5 (3-4-5 triangle), or 1:4/π
- Get link
- X
- Other Apps



Comments
Post a Comment