Force
A force is a push or pull upon an object resulting from the object's interaction with another object. Whenever there is an interaction between two objects, there is a force upon each of the objects. Forces only exist as a result of an interaction.
A force has both magnitude and direction and thus, it is a vector quantity.
 |
Force has both magnitude and direction
Photo by: fizkes on iStock |
When two forces do not have the same line of action, the magnitude and direction of the resultant force may be found by a procedure called vector addition of forces.
There are two graphical methods of performing vector addition, known as the triangle of forces method and the parallelogram of forces method.
 |
ADDITION OF VECTORS
Photo by: Mitu B |
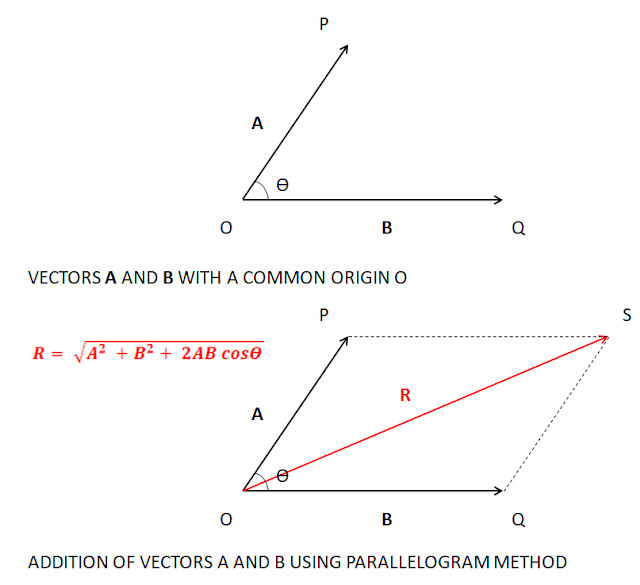
Law of parallelogram of forces
The law of parallelogram of forces states that if two vectors acting on a particle at the same time be represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point their resultant vector is represented in magnitude and direction by the diagonal of the parallelogram drawn from the same point.
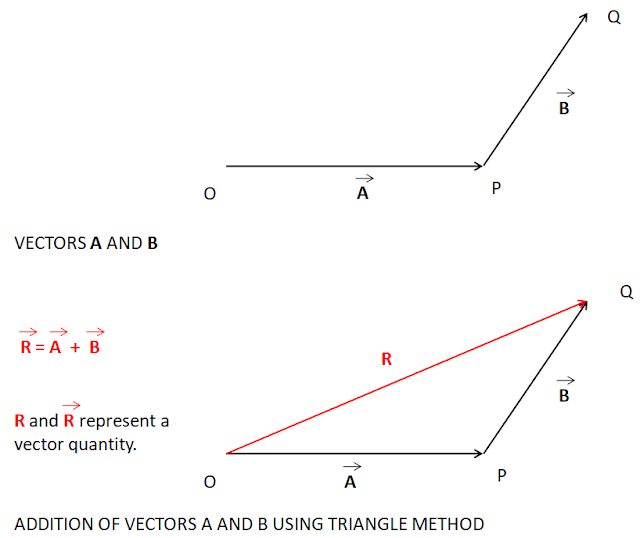
Law of triangle of forces
If two forces acting at a point are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then the closing side of the triangle taken in the reversed order represents the resultant of the forces in magnitude and direction.
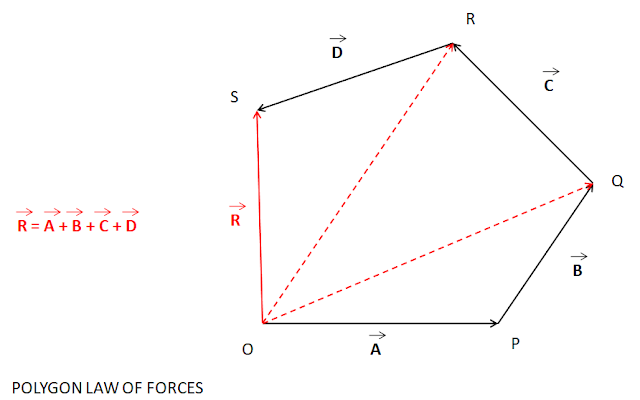
Polygon Law of forces
If a number of forces acting simultaneously on a particle be represented in magnitude and direction by the sides of a polygon taken in order, their resultant may be represented in magnitude and direction by the closing side of the polygon taken in opposite order.
Resolution of forces
 |
Resolution of forces |
A given force F can be resolved into (or replaced by) two forces, which together produces the same effects that of force F. These forces are called the components of the force F. This process of replacing a force into its components is known as resolution of a force into components.
A force can be resolved into two components, which are either perpendicular to each other or inclined to each other.
If the two components are perpendicular to one another, then they are known as rectangular components and when the components are inclined to each other, they are called as inclined components.
Resultant of number of concurrent coplanar forces
Source:
Coplanar Force - an overview | ScienceDirect Topics
When all forces are acting in the same plane, they are called coplanar.
When forces act at the same time and at the same point, they are called concurrent/forces.
For forces acting in the same direction and having the same line of action, the single force having the same effect as both of the forces, called the resultant force or just the resultant, is the arithmetic sum of the separate forces.
The x-component of the resultant is equal to the summation of forces in the x-direction.
Rx=
ΣFx
The y-component of the resultant is equal to the summation of forces in the y-direction.
Ry=
ΣFy
Therefore, Resultant force will be
R
= (Rx2+Ry2)1/2
tanθx
= Ry/Rx
Condition of equilibrium
First Condition of Equilibrium
For an object to be in equilibrium, it must be experiencing no acceleration. This means that both the net force and the net torque on the object must be zero.
The sum or resultant of all external forces acting on the body must be equal to zero.
Mathematically,
ΣF= 0,
ΣFx= 0, ΣFy= 0, ΣFz= 0
Second Condition
The second condition of static equilibrium says that the net torque acting on the object must be zero.
The sum or resultant of all external torques from external forces acting on the object must be zero.Mathematically,
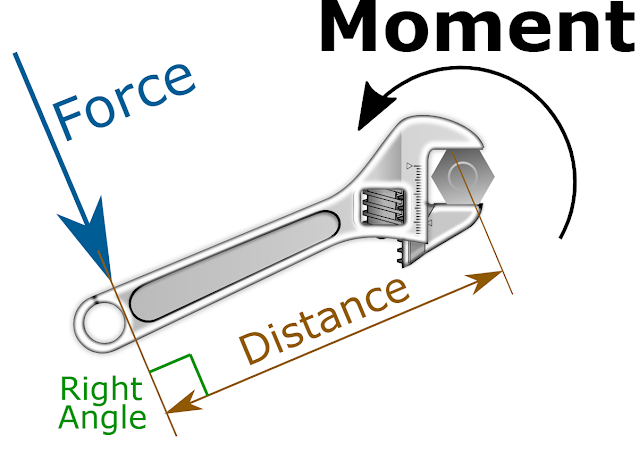
Moment of force
A moment of a force, or a torque, is a measure of a force's tendency to cause a body to rotate. The moment depends on both the force, and on the position at which the force acts.
Moment and arm of couple
The two equal and opposite forces, whose lines of action are different, form a couple.
The perpendicular distance between the lines of action of two equal and opposite forces is known as arm of the couple.
The magnitude of the couple (i.e. moment of a couple) is the product of one of the forces and the arm of the couple.
Theorems on couples.
1. The algebraic sum of the moments of two forces forming a couple about any plane is constant and equal to the moment of couple
2. Two couples equal in magnitude but opposite in direction, acting on a rigid body balance each other.
3. The couple on a rigid body remained unchanged if it is transferred to any plane to its own.
4. Any number of the couples in the same plane acting on a rigid body are equivalent to a single couple whose moment is equal to the algebraic sum of the moments of the couples.
5. A force and a couple acting in the same plane upon a rigid body are equivalent to a single force, equal and parallel to the original single force.
6. The moment of the couple of three forces acting on a rigid body represented in a magnitude, direction and the line of action by the sides of the triangle is equal to the twice the area of the triangle .
Hope you enjoyed the article | Click
here to follow the blog
Click
here to read similar posts
Click
here to see my substandard artwork 🙈









Comments
Post a Comment