GATE ARCHITECTURE 2021 -PART 1

GATE AR PAPER 2021 SOLVED PART 2

GATE AR PAPER 2021 SOLVED PART 3

General  Aptitude

Q.1      (i)         Arun and Aparna are here.

(ii)        Arun and Aparna is here.

(iii)       Arun’s families is here.

(iv)       Arun’s family is here.

Which of the above sentences are grammatically CORRECT?

(A)  (i) and (ii)
(B)   (i) and (iv)
(C)   (ii) and (iv)
(D)  (iii) and (iv)

Explanation: A sentence that begins with noun A (here, Arun) and noun B (here, Aparna) should be followed by a plural form of the verb. Family being a collective noun, it should take a singular verb.

Q.2 

The mirror image of the above text about the x- axis

 

Explanation:

Q.3      Two identical cube shaped dice each with faces numbered 1 to 6 are rolled simultaneously. The probability that an even number is rolled out on each dice is:

(A)  1/36
(B)   1/12
(C)   1/8
(D)  1/4

Explanation: Probability that first dice has even number= P(first even)= 3/6

Probability that second dice has even number= P(second even)= 3/6

P(both even)= (3/6)*(3/6)= ¼

Q.4      Ꚛ and ʘ are two operators on numbers p and q such that pʘq=p-q, and pꚚq=pxq Then, (9ʘ(6Ꚛ7))ʘ(7Ꚛ(6ʘ5))=

(A)  40
(B)   -26
(C)   -33
(D)  -40

Explanation: (9ʘ(6Ꚛ7))ʘ(7Ꚛ(6ʘ5))= (9-(6*7))-(7*(6-5))= (9-42)-(7*1)= -33-7= -40

Q.5      Four persons, P,Q,R and S are to be seated in a row. R should not be seated at the second position from the left end of the row. The number of distinct seating arrangements possible is:

(A)  6
(B)   9
(C)   18
(D)  24

Explanation: Total number of distinct arrangements= 18 (4 each for P,Q,S and 6 for R)

Starting with P

PQRS,PQSR,PSQR,PSRQ

Starting with Q

QPRS,QPSR,QSPR,QSRP

Starting with R

RPQS,RPSQ,RQPS,RQSP,RSPQ,RSQP

Starting with S

SPQR,SPRQ,SQPR,SQRP

Q.6      On a planar field, you travelled 3 units East from a point O. Next you travelled 4 units South to arrive at point P. Then you travelled from P in the North-East direction such that you arrive at a point that is 6 units East of point O. Next, you travelled in the North-West direction, so that you arrive t point Q that is 8 units North of point P.

The distance of point Q to point O, in the same units, should be

(A)  3
(B)   4
(C)   5
(D)  6

Explanation: As shown through the image and using Pythagoras theorem,

Distance of point Q to O =  = 5

Q.7      The author said, “Musicians rehearse before their concerts. Actors rehearse their roles before the opening of a new play. On the other hand, I find it strange that many public speakers think they can just walk on to the stage and start speaking. In my opinion, it is no less important for public speakers to rehearse their talks.”

Based on the above passage, which one of the following is TRUE?

(A)  The author is of the opinion that rehearsing is important for musicians, actors and public speakers.
(B)   The author is of the opinion that rehearsing is less important for public speakers than for musicians and actors.
(C)   The author is of the opinion that rehearsing is more important only for musicians than public speakers.
(D)  The author is of the opinion that rehearsing is more important for actors than musicians.

Q.8      1. Some football players play cricket.

            2. All cricket players play hockey.

Among the options given below, the statement that logically follows from the two statements 1 and 2 above, is:

(A)  No football player plays hockey.
(B)   Some football player play hockey.
(C)   All football player play hockey.
(D)  All hockey players play football.

Q.9     

In the figure shown above, PQRS is a square. The shaded portion is formed by the intersection of sectors of circles with radius equal to the side of the square and centers at S and Q.

The probability that any point picked randomly within the square falls in the shaded area is

(A)  4 - π/2
(B)   ½
(C)   π/2 - 1
(D)  π/4

Explanation: Probability of an event, P(A)=Number of favourable outcome(fA)/ Total Number of favourable outcome(TA)

Number of favourable outcomes = 2*(Area of quadrant of circle PSR – Area of triangle PRS)= 2*((πr²/4)-1/2(r*r)

Number of total outcomes= r²

P(A)= [2*((πr²/4)-1/2(r*r)]/ r²⁼ π/2 - 1

 

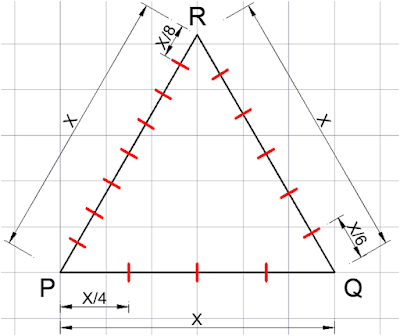
Q.10    In an equilateral triangle PQR, side PQ is divided into four equal parts, side QR is divided into six equal parts and side PR is divided into eight equal parts. The length of each subdivided part in cm is an integer.

The minimum area of the triangle PQR possible, in cm² is

(A)  18
(B)   24
(C)   488
(D)  144

Explanation: Since the length of each subdivided part is an integer, x should be LCM of 4,6 and 8. So x=24.

Area of an equilateral triangle= ½(base*height) = ( /4) x² = ( /4)*(24)²= 144

 

 

 

Click here to read similar posts 

Click here to see my substandard artwork 🙈